Setki układów elektrycznych i elektronicznych w nowoczesnych samochodach, częściowa i całkowita autonomia pojazdów, rozwiązania typu V2X (ang. Vehicle to Everything) – wszystko to sprawia, że współczesne samochody są coraz bardziej rozbudowane, ale także podatne na awarie, a producenci pojazdów nie ustają w dążeniu do poprawy bezpieczeństwa, które stało się bezwzględnym priorytetem.
Firmy z branży motoryzacyjnej z całego świata na bieżąco dostosowują swoje procesy do oczekiwań producentów samochodów albo już produkują wyroby zgodne z wymaganiami ISO 26262. Aktualnie, bezpieczeństwo przestało być luksusem i stało się koniecznością. W tej części serii skoncentruję się na przedstawieniu podstawowych algorytmów sterowania napędami (które coraz częściej można spotkać m.in. w branży automotive) oraz tym, jak zaimplementować takie rozwiązania na stanowisku testowym i porównam wyniki symulacyjne z rzeczywistymi.
W kolejnych artykułach z serii będę koncentrował się na pozostałych istotnych tematach związanych z napędami elektrycznymi, począwszy od sterowania przemiennikami częstotliwości, przez układy pomiarowe, metody estymacji i obserwacji zmiennych stanu, analizę uszkodzeń, a kończąc na diagnostyce aktywnej oraz sterowaniu odpornym.
Wiedza teoretyczna, którą przedstawię, jest dosyć uniwersalna i może być stosowana w różnych gałęziach technologicznych, zarówno w szeroko pojętym automotive – pojazdach hybrydowych, elektrycznych czy autonomicznych – ale także w rozwiązaniach przemysłowych (taśmociągi, dźwigi, dźwignice, suwnice itd.), a nawet domowym sprzęcie AGD np. pralkach czy suszarkach.
Uprzedzę Was przy okazji, że w tekście mogą pojawić się trudniejsze fragmenty, ale zachęcam do zapoznania się z nimi, ponieważ pozwolą na łatwiejsze zrozumienie kolejnych i ciekawszych publikacji.
Metody i struktury sterowania silnikami elektrycznymi
Współczesne układy napędowe wykorzystywane między innymi w pojazdach elektrycznych i hybrydowych, mogą być sterowane przy wykorzystaniu różnych algorytmów. Coraz częściej stosowane są wysokiej jakości regulowane napędy elektryczne VFD (ang. Variable Frequency Drives) zasilane z przemienników częstotliwości, które są w stanie spełniać surowe wymagania funkcjonalne, wydajnościowe oraz bezpieczeństwa.
Bez względu jaką metodą sterowania się posłużymy, zawsze będziemy starać się kontrolować moment elektromagnetyczny w sposób pośredni lub bezpośredni. Moment silnika może być regulowany na wiele sposobów, które zależą od wyboru elektromagnetycznych zmiennych stanu (x1e i x2e). Dla przykładu bardzo ogólna zależność na moment silnika indukcyjnego jest wyrażona jako:
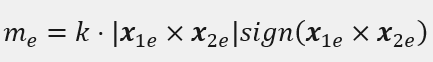
Zmienne te możemy w pewnym stopniu wskazywać dowolnie, ale musimy bazować na modelu matematycznym maszyny. Wybór wielkości sterujących momentem, uproszczenia zależności matematycznych i modelu silnika oraz dodatkowo przyjęte warunki, decydują o właściwościach statycznych i dynamicznych napędu.
Aktualny generalny podział istniejących metod i struktur sterowania silnikami elektrycznymi przedstawiono na Ryc. 1., a najogólniej można podzielić go na:
- układy zewnętrzne – sterowanie w strukturze otwartej,
- układy wewnętrzne – sterowanie w strukturze zamkniętej.
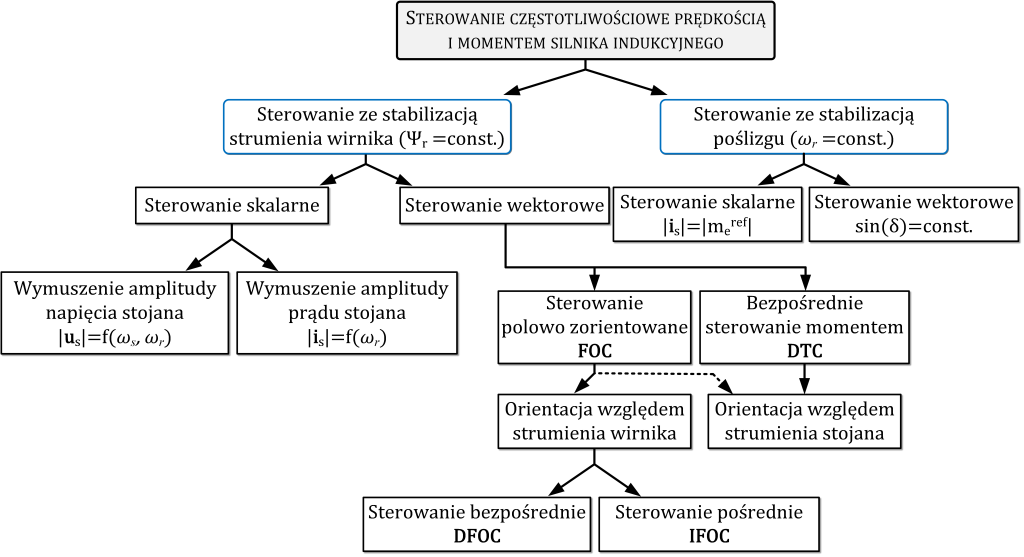
W systemach sterowania zewnętrznego w stanach nieustalonych silnika powstają niekontrolowane procesy przejściowe, co skutkuje powstawaniem słabo tłumionych oscylacji i utykaniem silnika. Napędy sterowane w ten sposób nie mogą być stosowane w aplikacjach wymagających częstych zmian obciążenia i częstotliwości (prędkości silnika).
Natomiast struktury sterowania wewnętrznego (ze sprzężeniami zwrotnymi) stosowane są zazwyczaj w aplikacjach wymagających stabilizacji prędkości i bardzo dobrych właściwości dynamicznych. W tym celu wykorzystywane są zaawansowane algorytmy regulacji oraz szybkie procesory sygnałowe i precyzyjne układy pomiarowe, pozwalające na szybką kompensację uchybów pomiędzy wartościami zadanymi i mierzonymi.
Ja skoncentruję się mocniej na tych ostatnich, określanych także jako metody sterowania wektorowego, ponieważ są coraz popularniejsze, dużo bardziej skomplikowane, posiadają wiele możliwości modyfikacji i rozszerzenia funkcjonalności, a co za tym idzie – są ciekawsze.
Metody wektorowe
Metody wektorowe nie bazują na wartościach poszczególnych wielkości (skalarach) tylko, jak sama nazwa wskazuje, na ich wektorach. Dlatego pierwszym krokiem jest wyznaczenie zależności różniczkowo-całkowych maszyny elektrycznej i stworzenie jej modelu matematycznego (przyjmując pewne założenia i uproszczenia), a następnie zapis tych równań za pomocą wektora przestrzennego w wirującym układzie współrzędnych.
Zabieg ten pozwala na zmniejszenie liczby działań różniczkowych oraz umożliwia prezentację modelu w różnych układach współrzędnych prostokątnych. W sterowanym wektorowo silniku prądu przemiennego mierzone są trójfazowe wielkości zmienne, które ze stacjonarnej płaszczyzny odniesienia mogą zostać zespolone w pojedynczy wektor wirujący w czasie.
Nieruchomy układ trójfazowy opisuje się wektorowo w tak zwanym systemie współrzędnych A-B-C, w którym składowe wektora są rozmieszczone co 120 stopni (Ryc. 2a). Wirujący wektor łatwiej jest przedstawić w układzie dwuosiowym, więc sygnały w dziedzinie czasu przekształca w dwie składowe w tak zwanym ortogonalnym systemie α-β.
Układ ten odnosi się do stojana (nieruchomej części silnika), przy czym składowa α jest zrównana ze składową A układu A-B-C, a składowa β jest do niej prostopadła (Ryc. 2b). Nadal mamy do czynienia z wektorem zmiennym w czasie, dlatego w kolejnym kroku stosuje się kolejną transformację, ale tym razem przechodzimy do układu współrzędnych d-q (x-y) wirującego współosiowo z wirnikiem (częścią ruchomą silnika), jak na Ryc. 2c.
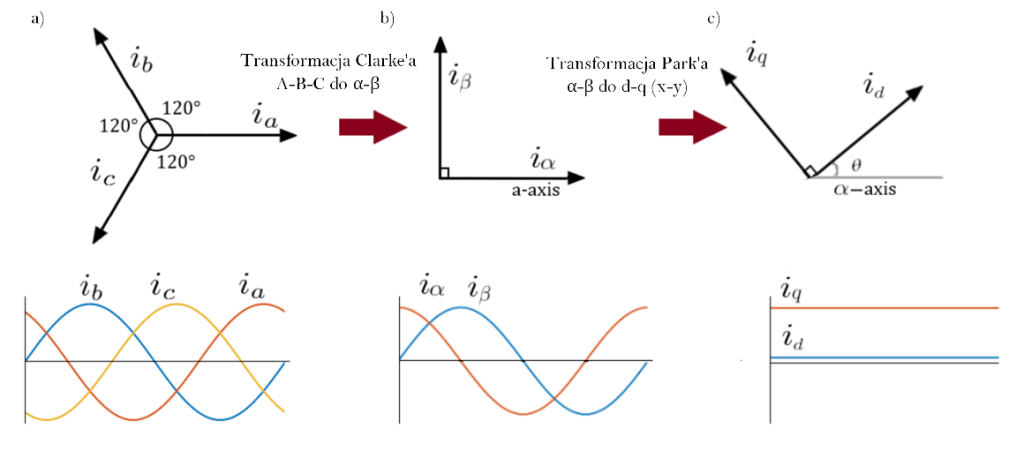
Aby poprawnie wyznaczyć tę płaszczyznę, potrzebny jest kąt θ, który dla silników synchronicznych otrzymuje się bezpośrednio z czujnika położenia wirnika. Jednakże nasz przypadek dotyczy silnika indukcyjnego (asynchronicznego), dlatego musimy dodatkowo uwzględnić poślizg, czyli względną różnicą między prędkością obrotową wirnika a prędkością wirowania pola magnetycznego, która wynika z takich paramentów jak liczba par biegunów czy częstotliwość prądu zasilającego.
Położenie wirnika musimy zatem obliczyć, wykorzystując matematyczne zależności obserwatora stanu silnika. O metodach odtwarzania wielkości trudnomierzalnych, estymatorach i obserwatorach stanu opowiem więcej w oddzielnej części serii. Posiadając kąt położenia wirnika, jesteśmy w stanie przejść z jednego układu współrzędnych na drugi i z powrotem. Właśnie te zależności (określane jako transformacje Clarke’a i Parka) są kluczem sterowania wektorowego. Wdrożenie różnych systemów odniesienia znacząco upraszcza nam analizę i obliczenia całego układu, a w konsekwencji pozwala na efektywne sterowanie silnikiem, ponieważ przemienne przebiegi prądu i napięcia przedstawiane są w warunkach stanu ustalonego.
W zależności od wyboru sygnałów (wektorów) sterujących możemy wyróżnić dwie kluczowe metody wektorowe z modulacją wektorową przekształtnika:
- struktura sterowania polowo-zorientowanego (DRFOC – ang. Direct Rotor Field Oriented Control),
- struktura bezpośredniego sterowania momentem elektromagnetycznym (DTC – ang. Direct Torque Control).
W obu przypadkach główna idea polega na oddzielnym sterowaniu momentem elektromagnetycznych i strumieniem uzwojenia w silniku, co pozwala uzyskać wysoką dokładność regulacji prędkości obrotowej.
Struktura sterowania polowo-zorientowanego
Pomijając skomplikowane wzory i zależności matematyczne, główna idea działania pierwszej z metod polega na wydzieleniu składowej czynnej wektora prądu stojana isy (decydującej o momencie elektromagnetycznym) oraz biernej isx (odpowiedzialnej za strumień).
Przyjmujemy, że nasz układ współrzędnych wiruje współbieżnie z wektorem strumienia skojarzonego wirnika ψr(oś x z Ryc. 3a). Wektor prądu stojana is, mierzony w układzie A-B-C, może zostać rozłożony na dwie składowe α-β oraz dwie składowe prostokątne is = [isx, isy]. Wydzielenie tych prądów odbywa się z wykorzystaniem układu odtwarzającego (estymatora) wektor strumienia wirnika, na podstawie informacji o położeniu wektora strumienia wirnika. Wykorzystując informację o położeniu wirnika, dokonywana jest transformacja Clarke’a wektora prądu stojana z układu fazowego A-B-C do stacjonarnego α-β i następnie Parka do docelowego układu x-y.
Graficzne przedstawienie położenia wektorów w układach współrzędnych przedstawiono na Ryc. 3a.
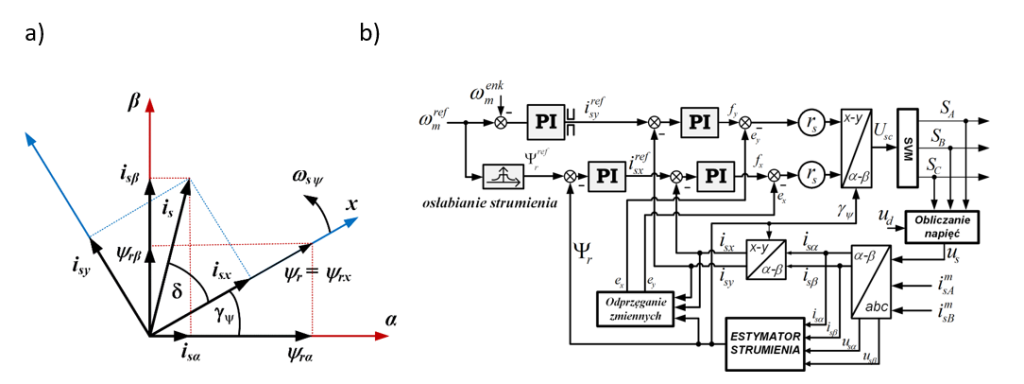
W praktyce dwie przetransformowane składowe prądu są regulowane oddzielnie sterownikami typu PI, a sygnałami wyjściowymi są składowe wektora napięcia stojana we współrzędnych x-y, które po transformacji powrotnej do układu α-β przekazywane są na wejście modulatora przekształtnika częstotliwości.
W klasycznej strukturze wykorzystujemy cztery regulatory PI:
- prędkości kątowej,
- strumienia wirnika,
- składowej isx prądu stojana,
- składowej isy prądu stojana.
Schemat ideowy umieściłem na Ryc. 3b. Oczywiście tę strukturę możemy modyfikować w zależności od tego, którym sygnałem mamy zamiar sterować. Popularne rozwiązania umożliwiają między innymi: dodanie kolejnej pętli regulacji i sterowanie położeniem wirnika maszyny czy bezpośrednie zadawanie wartości prądów isx, isy (eliminacja pętli prędkości i strumienia.
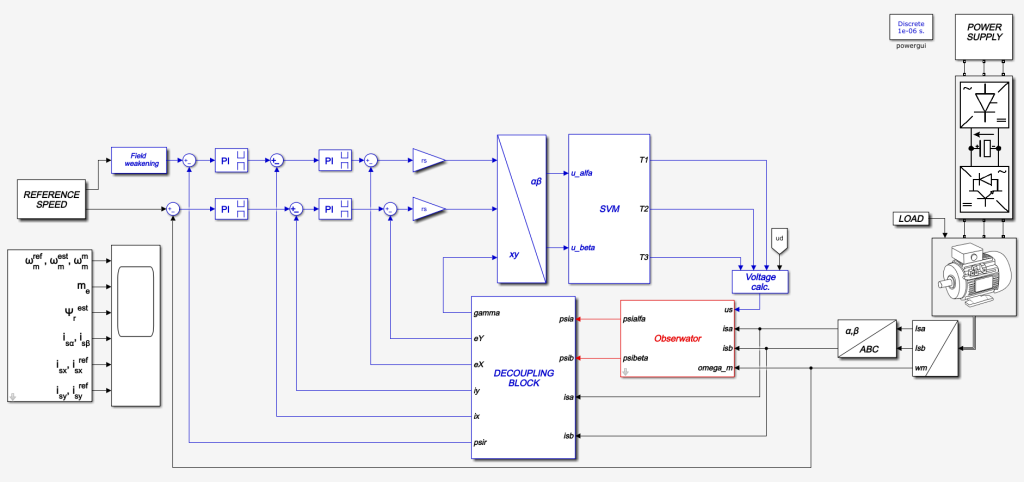
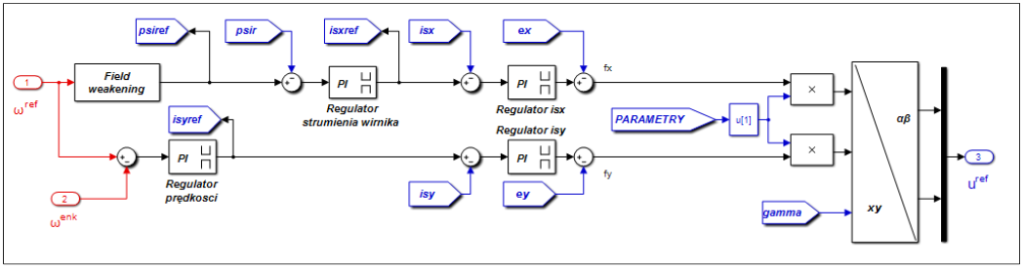
Na Ryc. 4 zaprezentowano strukturę całego modelu sterowania DRFOC z pętlą regulacji prędkości silnika, zrealizowaną w środowisku Matlab/Simulink, którą wykorzystywałem do testów symulacyjnych.
Struktura bezpośredniego sterowania momentem elektromagnetycznym
Drugą najbardziej popularną metodą sterowania jest bezpośrednie sterowanie momentem elektromagnetycznym (ang. DTC – Direct Torque Control), nazywane również DTFC (ang. Direct Torque and Flux Control). Metoda ta zdobyła swoją popularność dzięki zapewnieniu napędom elektrycznym bardzo dobrej dynamiki momentu i strumienia, brakowi transformacji współrzędnych oraz małej ilości parametrów wymagających strojenia.
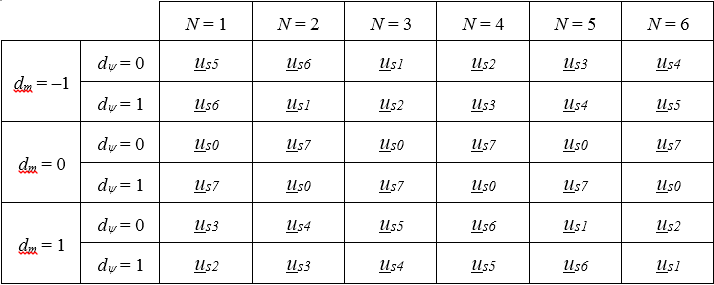
Główna idea algorytmu sterowania sprowadza się do bezpośredniego wyznaczania sygnałów sterujących przełączaniem poszczególnych łączników przemiennika częstotliwości na podstawie sygnałów z regulatorów histerezowych strumienia i momentu oraz tablicy przełączeń (Ryc. 5).
Strategia sterowania wynika z jednej z zależności na moment silnika indukcyjnego i polega na jednoczesnym wpływaniu na wartość momentu elektromagnetycznego oraz na wartość amplitudy strumienia magnetycznego:
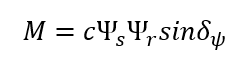
gdzie:
c – stała zależna od parametrów silnika,
Ψs, Ψr – strumień skojarzony stojana i wirnika,
δψ – kąt pomiędzy wektorami strumienia stojana i wirnika.
Przyjmuje się, że wektor przestrzenny strumienia skojarzonego wirnika ma stałą amplitudę i prędkość wirowania, więc kształtowanie momentu polega na sterowaniu położeniem wektora przestrzennego strumienia stojana. Zakładając brak bezpośredniej ingerencji w wartość prądu (sterowanie nadążne), regulacji dokonujemy poprzez odpowiednie zasilanie uzwojeń stojana silnika:
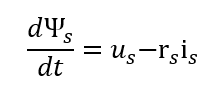
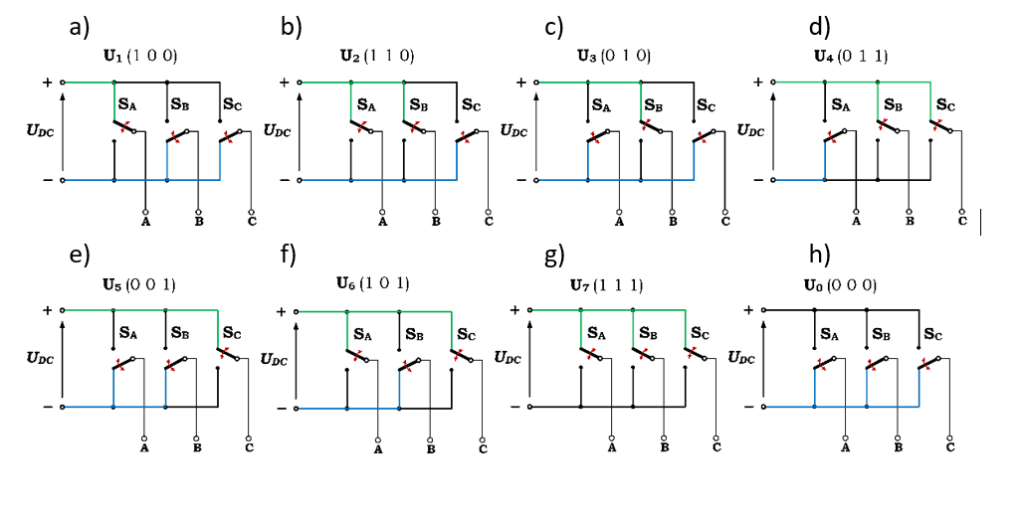
W falowniku mamy dostępne sześć aktywnych wektorów napięcia oraz dwa zerowe (000 i 111) – znajdziecie je na Ryc. 6. Użycie jednego z nich powoduje przyrost (lub redukcję) wektora przestrzennego strumienia skojarzonego stojana w kierunku zgodnym z użytym wektorem napięcia stojana.
W metodzie DTC stosuje się regulatory komparatorowe porównujące wartości zadane z mierzonymi: dwupołożeniowy strumienia oraz trójpołożeniowy momentu o szerokości strefy równej 2Hm.
Sygnały wyjściowe komparatorów dψ oraz dm określone są jako:
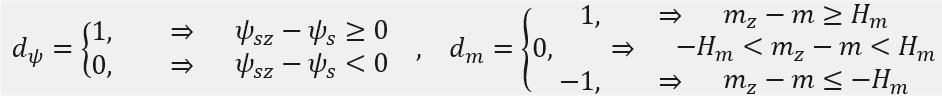
Ponadto, konieczne jest wyznaczenie położenia wektora przestrzennego strumienia skojarzonego stojana z dokładnością do jednego z sześciu sektorów – N. Na podstawie sygnałów wyjściowych komparatorów dψ, dm oraz numeru sektora N, z tablicy przełączeń (Ryc. 5) wybierany jest odpowiedni wektor napięcia stojana.
W ten sposób kontrolujemy długość wektora strumienia stojana oraz jego położenie względem wektora strumienia wirnika, wpływając jednocześnie na wartość momentu elektromagnetycznego generowanego przez silnik.
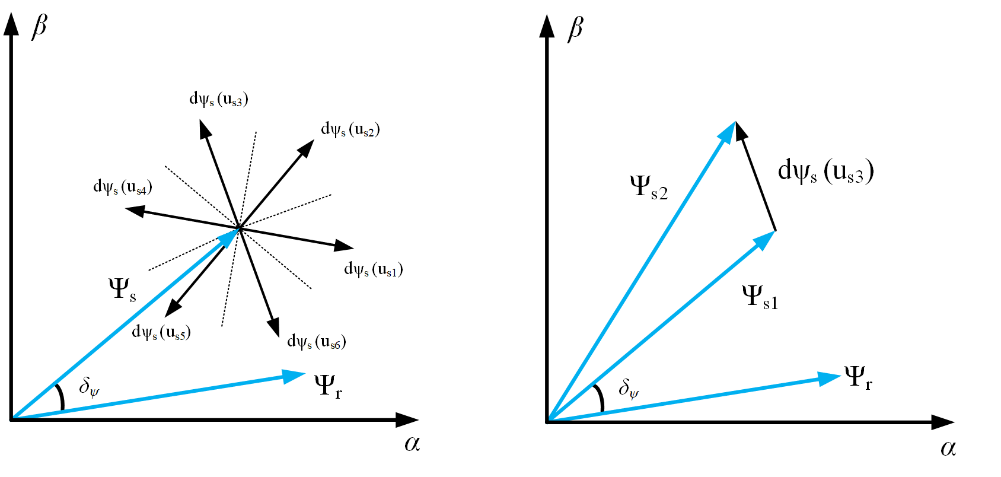
Przykład: jeżeli wektor strumienia stojana znajduje się aktualnie w sektorze N=2, oraz gdy wartość momentu i strumienia są za małe w stosunku do wartości zadanych (regulatory histerezowe zwracają na wyjściu: dm=1, dψ=1), to zostanie wybrany wektor napięcia us3, który spowoduje zwiększenie amplitudy wektora przestrzennego strumienia skojarzonego stojana oraz zwiększenie kąta δψ, czyli zwiększenie momentu (przyspieszenie silnika) – Ryc. 7.
Klasyczna postać metody DTC (z tzw. tablicą przełączeń) została rozwinięta oraz poprawiona w celu eliminacji jej podstawowych wad, tj. pulsacji strumienia i momentu oraz zmiennej częstotliwości przełączeń łączników przekształtnika napięcia.
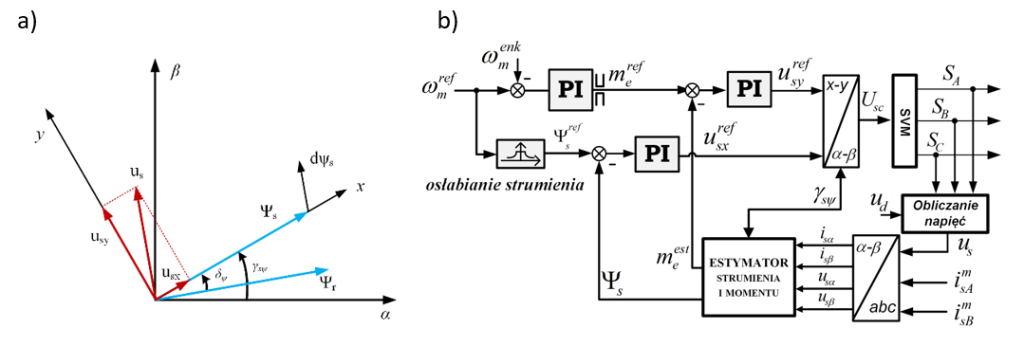
Przede wszystkim regulatory histerezowe strumienia i momentu oraz tablica przełączeń zostały zastąpione regulatorami liniowymi PI oraz modulatorem wektorowym (SVM – ang. Space Vector Modulation) – układ sterowania tranzystorami przemiennika częstotliwości. Główna idea sterowania pozostaje więc bez zmian, a kluczowa modyfikacja dotyczy wprowadzenia transformacji składowych wektora napięcia stojana us = [usx, usy] do układu współrzędnych x-y – Ryc. 8a.
Zadane sygnały strumienia stojana i momentu elektromagnetycznego są porównywane z wartościami estymowanymi, a uzyskane uchyby podawane są na wejścia regulatorów PI. Sygnały wyjściowe regulatorów, stanowią wartości zadane napięć stojana usx i usy, które po transformacji do stacjonarnego układu α-β wykorzystywane są do obliczania czasów załączeń tranzystorów w bloku modulatora SVM.
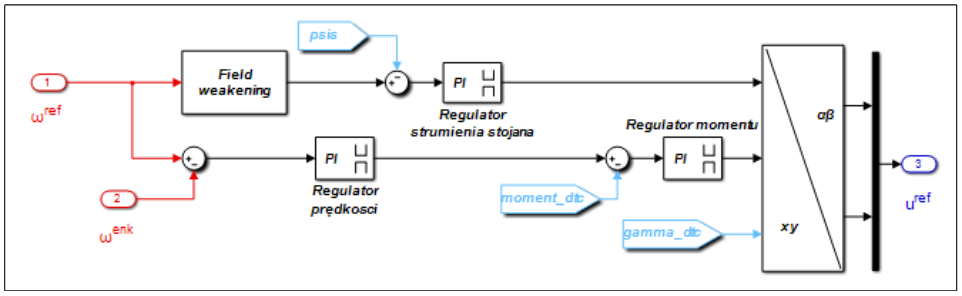
Schemat ideowy struktury z dodatkową pętlą regulacji prędkości przedstawiono na Ryc. 8b.
Metoda DTC-SVM z pozytywnym skutkiem łączy zalety struktury polowo-zorientowanej oraz bezpośredniego sterowania momentem z tablicą przełączeń, zapewniając doskonałą dynamikę oraz stabilność pracy układu napędowego. Metoda ta z powodzeniem wykorzystywana jest w napędach bezczujnikowych oraz w złożonych aplikacjach przemysłowych, zwłaszcza w układach wymagających szybkich i kontrolowanych zmian momentu elektromagnetycznego.
Implementacja i weryfikacja w praktyce
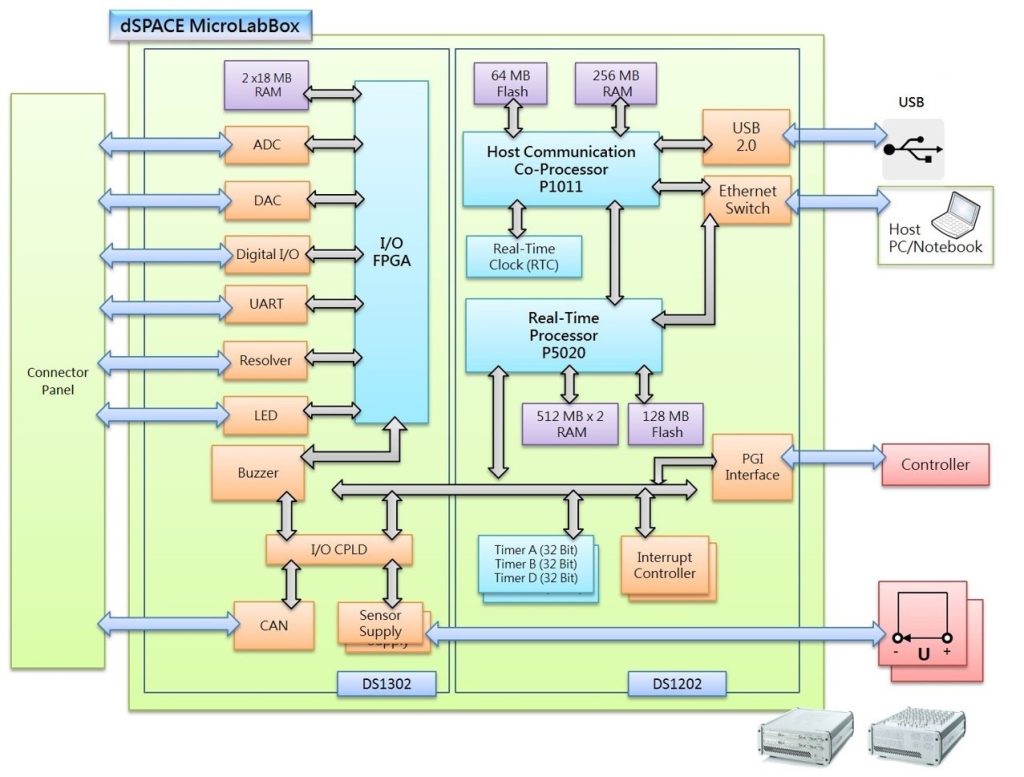
Praktyczna implementacja i weryfikacja odbywają się na stanowisku testowym i w moim przypadku składało się ono z komputera PC z zainstalowanym środowiskiem programistycznym i operatorskim ControlDesk. Do realizacji badań eksperymentalnych wykorzystywałem kartę szybkiego prototypowania DS1202 zaimplementowaną na platformie MicroLabBox firmy dSPACE GmbH, która połączona była z komputerem złączem ethernetowym.
Platforma MicroLab Box (Ryc. 9) posiada dwurdzeniowy procesor czasu rzeczywistego o częstotliwości taktowania 2 GHz (Freescale PowerPC QorIQ P5020) oraz zintegrowany, programowalny układ logiczny FPGA firmy Xilinx (Kintex-7 XC7K325T) przeznaczony dla bardziej wymagających aplikacji. Jednostka MicroLabBox zawiera ponad 100 analogowych (BNC) oraz cyfrowych portów wejściowych i wyjściowych, a ponadto obsługuje protokoły komunikacyjne CAN i Ethernet oraz dedykowane wejścia dla resolwerów i innych przetworników położenia.
Wyraźnie widać, że platforma ta jest znacznie przewymiarowana i dlatego jest świetnym rozwiązaniem dla pojedynczych i skomplikowanych projektów rozwojowych i prototypowych oraz rozbudowanych systemów napędowych.

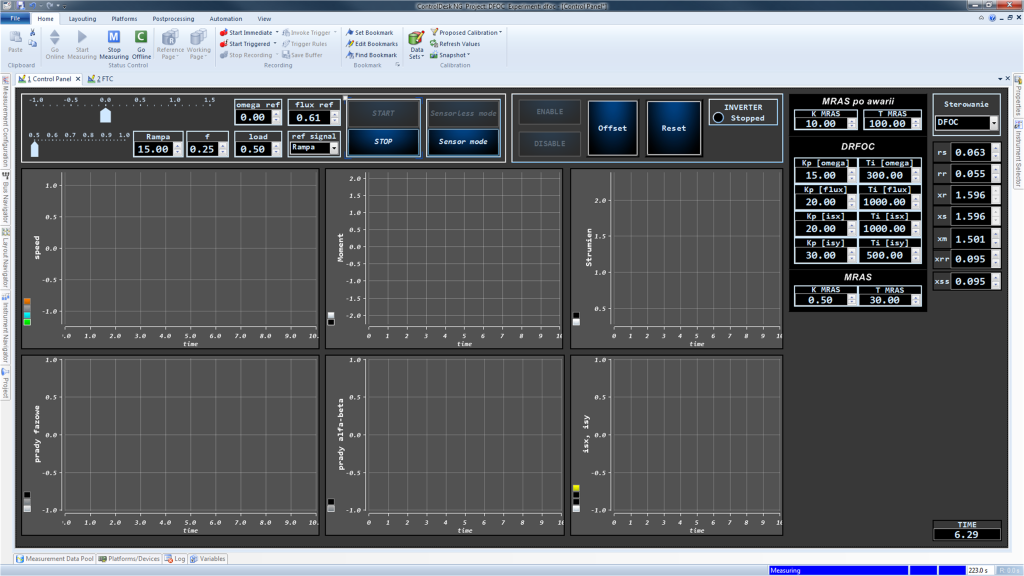
Środowiskiem programistycznym, którym się posłużyłem do modelowania układów sterowania (Rysc. 10 i 11), jest MATLAB Simulink wraz z bibliotekami specjalistycznymi (ang. RTI – Real-Time Interface). Zaimplementowane na karcie procesorowej programy były kontrolowane za pośrednictwem aplikacji zaprojektowanej w ControlDesk Next Generation. Pozwala ona na stworzenie pulpitu operatorskiego umożliwiającego wizualizację graficzną, dostęp i zmianę parametrów układu sterowania w czasie realizacji procesu bez konieczności ponownej kompilacji i generacji kodu. Ponadto umożliwia ona monitorowanie i rejestrowanie przebiegów zmiennych modelu w czasie rzeczywistym.
Na Ryc. 12 przedstawiono okno programu z układem sterowania polowo-zorientowanego.
Za pomocą platformy sterowane są dwa przekształtniki częstotliwości zasilające silniki firmy BESEL:
- indukcyjny napędzany SH 80X-4C (1,1 kW),
- indukcyjny pełniący funkcję maszyny obciążającej SH 80X-4D (1,5 kW).
Silnik obciążający zasilany jest z przekształtnika firmy TWERD (model MFC 710) o mocy 1,5 kW i sterowany wektorowo w strukturze momentowej. Wartość momentu obciążenia zadawana jest przez MicroLabBox i podawana na wejście analogowe (0-10V DC) przemiennika. Prędkość kątowa wirnika maszyny obciążającej jest mierzona za pomocą enkodera inkrementalnego firmy Kübler (model 8.5020.D54A.5000.0050). Schemat stanowiska laboratoryjnego został przedstawiony na rys. 13.
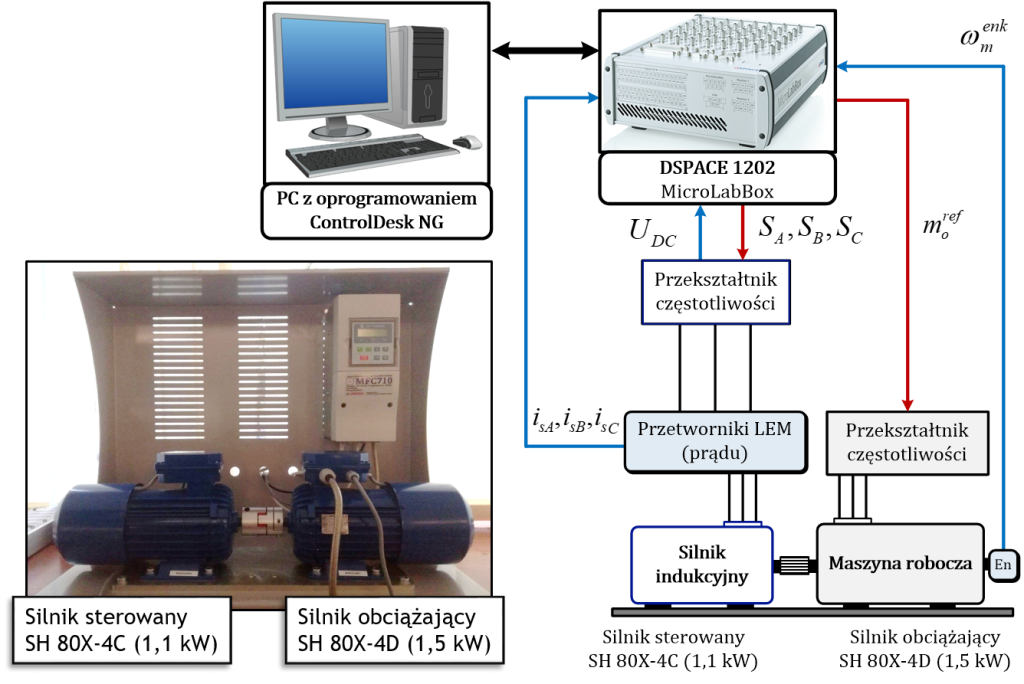
Informacja o napięciu zasilającym stojan maszyny obliczana jest na podstawie czasów załączeń tranzystorów przemiennika częstotliwości oraz napięcia w obwodzie pośredniczącym przekształtnika, mierzonego za pomocą przetwornika napięciowego firmy LEM. Wartości prądów stojana są uzyskiwane z pomiaru wykorzystującego dwa (lub trzy) hallotronowe przetworniki prądowe z zamkniętą pętlą sprzężenia firmy LEM. Aktualna wartość prędkości kątowej wirnika otrzymywana jest z enkodera inkrementalnego firmy Kübler (model 8.5020.D54A.5000.0050) o rozdzielczości 5000 impulsów na obrót.
Wyniki
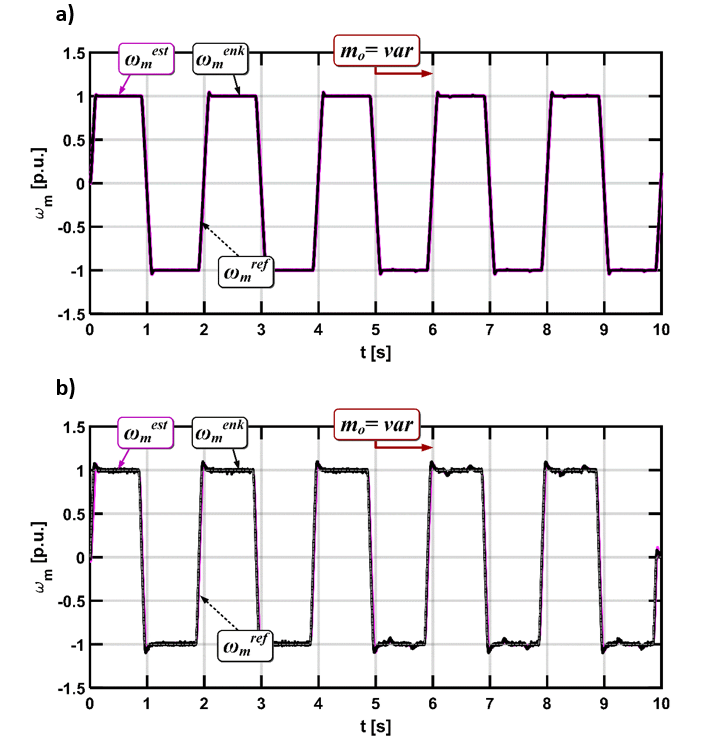
Poniżej możecie zapoznać się z przykładowymi przebiegami podstawowych sygnałów sterujących podczas pracy nawrotnej silnika w pełnym zakresie prędkości. Dodatkowo od 5-tej sekundy maszyna robocza jest obciążana, gdy znajduje się w stanie ustalonym.
Na pierwszy rzut oka możemy zauważyć, że w przypadku wyników rzeczywistych prędkość mierzona z enkodera jest bardziej poszarpana i widoczne są większe przeregulowania chwilę przed osiągnięciem wartości zadanej. W wynikach symulacyjnych wielkości mierzone niemal idealnie pokrywają się z żądanymi i ten fakt dotyczy wszystkich sygnałów.
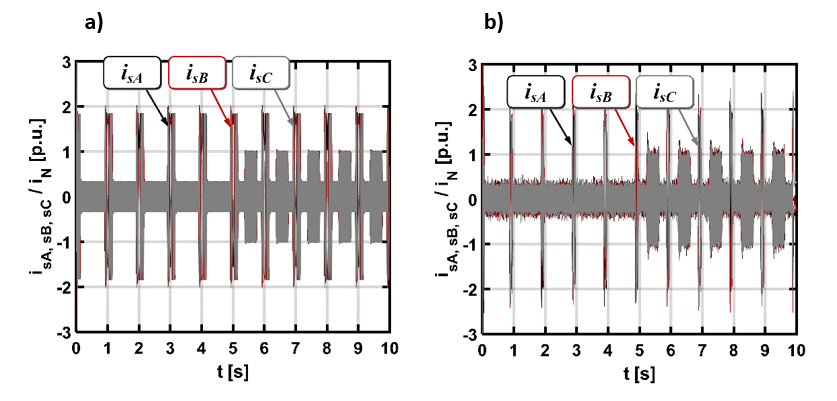
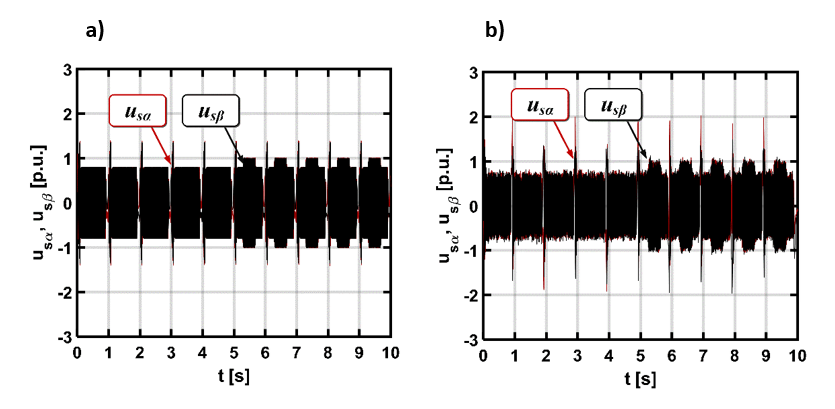
Największe szarpania i zakłócenia są oczywiście widoczne na przebiegach składowych wektora prądu i napięcia stojana, ponieważ te sygnały pobierane są z systemu pomiarowego i nie są bezpośrednio kontrolowane. Ponadto, przetworniki pomiarowe posiadają swoje niedoskonałości i asymetrie względem poszczególnych faz oraz są podatne na szumy i zakłócenia.
W przypadku prądów sterujących (isx, isy) sytuacja wygląda już dużo lepiej i jest wyraźnie widoczne, że obie wielkości są kontrolowane i pokrywają się z wartościami referencyjnymi.
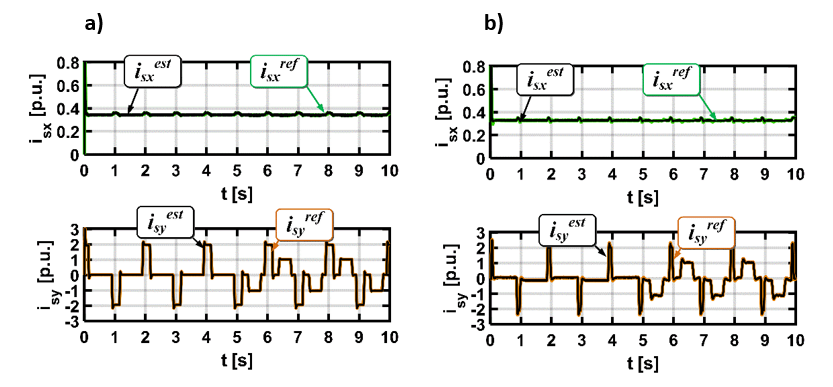
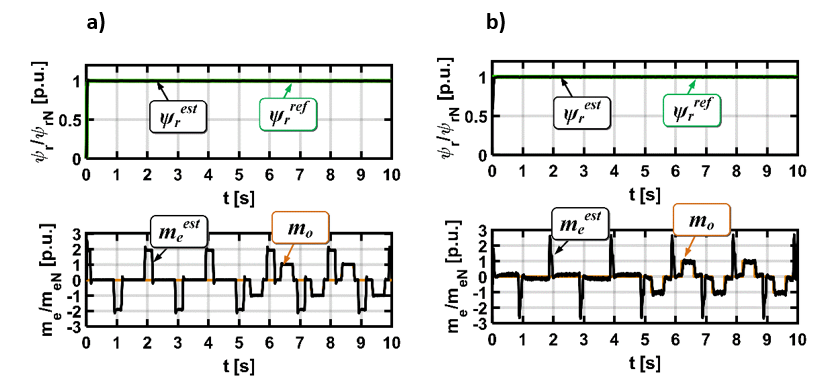
W sterowaniu polowo-zorientowanym w/w składowe prądu są ściśle związane z wartościami chwilowymi strumienia wirnika oraz momentu elektromagnetycznego. W pierwszym przypadku powinniśmy widzieć stałą wartość prądu isx i modułu strumienia przez cały okres pracy napędu. Natomiast przebiegi składowej isy oraz momentu są niemal identyczne i mogą różnić się jedynie proporcjonalnie wartościami.
Powyższe przykładowe przebiegi pokazują nam, że sterowanie wektorowe umożliwia rozwijanie dużego i stabilnego momentu obrotowego w całym zakresie prędkości znamionowej silnika. Ponadto, zespół napędowy regulowany w ten sposób charakteryzuje się wysoką dynamiką pracy przez co czas reakcji na zmianę obciążenia wału lub żądanej wartości prędkości jest bardzo krótki. Dlatego takie algorytmy sterowania spotykane są coraz częściej w branży automotive i nadal są rozwijane.
Mam nadzieję, że powyższy artykuł choć trochę przybliżył Wam zagadnienie precyzyjnego sterowania silnikami elektrycznymi. Jeżeli będziecie mieli dodatkowe pytania, to chętnie na nie odpowiem w komentarzach.
W kolejnej części przedstawię sposoby sterowania przekształtnikiem częstotliwości, w tym dobrze większości znaną metodę PWM, ale również bardziej skomplikowaną modulację wektorem przestrzennym SVM.
Literatura
Część teoretyczna została opracowana na podstawie poniższych pozycji literatury:
- Dybkowski M., Estymacja prędkości kątowej w złożonych układach napędowych – zagadnienia wybrane, Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Politechniki Wrocławskiej, Monografie, vol. 67, nr 20, 2013.
- Dybkowski M., Klimkowski K., Orłowska-Kowalska, T., Speed and current sensor fault-tolerant-control of the induction motor drive. W: Advanced control of electrical drives and power electronic converters / ed. by Jacek Kabziński. Cham: Springer, cop. 2017. s. 141-167. (Studies in Systems, Decision and Control, ISSN 2198-4182; vol. 75).
- Klimkowski K., Analiza układów napędowych z silnikami indukcyjnymi odpornymi na uszkodzenia czujników pomiarowych, Rozprawa Doktorska, Raporty Katedry Maszyn Napędów i Pomiarów Elektrycznych Politechniki Wrocławskiej. 2017, Ser. PRE; nr 10. 249 s.
- Orłowska-Kowalska T., Bezczujnikowe układy napędowe z silnikami Indukcyjnymi, Oficyna Wydawnicza Politechniki Wrocławskiej, Wrocław 2003.
- Tunia H., Kaźmierkowski M. P., Automatyka napędu przekształtnikowego, Państwowe Wydawnictwo Naukowe, 1987.
***
Jeśli interesuje Cię tematyka ISO i standaryzacji, zachęcamy do zapoznania się z artykułami naszych ekspertów: Functional Safety ISO 26262 – ASIL i metryki oraz Analiza porównawcza standardów rozwoju oprogramowania w odniesieniu do lotnictwa i pojazdów naziemnych.
















Zostaw komentarz