Wstęp do obliczeń kwantowych

W artykule przedstawię podstawowe pojęcia związane z obliczeniami na komputerze kwantowym. Nie będzie tu fizycznego opisu właściwości tych komputerów, lecz zaprezentuję matematyczne podstawy wykorzystywane przy obliczeniach kwantowych. Na koniec przybliżę Wam algorytm kwantowy. Jego założenia są jednymi z prostszych w świecie algorytmów i nie mają większego, praktycznego zastosowania.

Ideą tego wpisu jest pokazanie, jak za pomocą właściwości komputerów kwantowych można przyspieszyć czas działania algorytmu, którego czas wykonania jest stały, w przeciwieństwie do algorytmu klasycznego, którego czas wykonania może być wykładniczy.

Kilka słów wprowadzenia

Zanim przedstawię algorytm kwantowy, potrzebnych będzie trochę informacji wprowadzających.

Kubit

Jednostka informacji w obliczeniach kwantowych. Kubit ma wartość a∣0⟩ + b∣1⟩, gdzie a²+b²=1.∣0⟩, któremu odpowiada wektor $\left[\begin{array}{c}1\\ 0\end{array}\right]$, oraz ∣1⟩, któremu odpowiada wektor $\left[\begin{array}{c}0\\ 1\end{array}\right]$, są wektorami bazy standardowej $\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ .

a² jest to prawdopodobieństwo tego, że kubit osiągnie przy pomiarze wartość 0, a b² jest to prawdopodobieństwo otrzymania 1.

Bramka Hadamarda

Jest to logiczna bramka kwantowa działająca na jeden kubit.

Została następująco zdefiniowana:

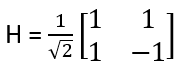
Ustawia ona standardowe wektory bazowe następująco:

1. jeśli kubit jest w stanie 0, to:

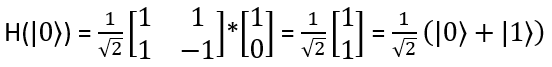
2. jeśli kubit jest w stanie 1, to:

Iloczyn tensorowy (Kroneckera)

Iloczyn tensorowy dwóch wektorów wygląda jak poniżej:

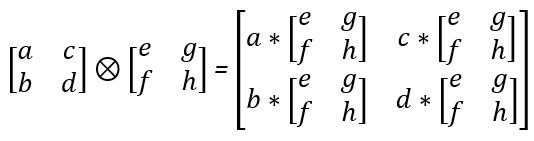
Mnożąc różne wektory bazy standardowej, otrzymujemy:

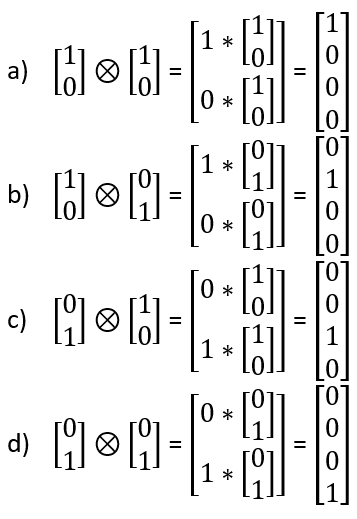
Używając iloczynu tensorowego dla dwóch kubitów,

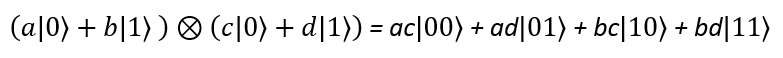
można uzyskać prawdopodobieństwo osiągnięcia czterech możliwych stanów.
W przypadku trzech kubitów istnieje 8 możliwych stanów.

Algorytm Deutscha-Jozsy

W tym momencie warto przedstawić algorytm Deutscha-Jozsy dla n równego 3.

Celem algorytmu jest stwierdzenie, czy dana funkcja, której argumenty mają wartość 0 lub 1, jest stała czy zbalansowana. Funkcja jest stała, gdy dla każdych argumentów przyjmuje zawsze wartość 0 lub 1. Funkcja jest zbalansowana, gdy dla połowy argumentów przyjmuje wartość 0, a dla połowy wartość 1. Możliwe wartości dla funkcji to:

1. Funkcja dla wszystkich argumentów przyjmuje wartość 0 – F(x₁, x₂,…, x_n)=0
2. Funkcja dla wszystkich argumentów przyjmuje wartość 1 – F(x₁, x₂,…, x_n)=1
3. Funkcja dla połowy argumentów przyjmuje wartości 0, a dla pozostałej połowy argumentów wartość 1

Ilość wejść możliwa dla tej funkcji wynosi 2ⁿ. Aby stwierdzić, czy funkcja jest stała lub zbalansowana w najgorszym przypadku potrzebne jest 2^n-1+1 wywołań funkcji dla różnych argumentów.

Przedstawiony algorytm kwantowy rozwiązuje ten problem zawsze w czasie stałym, więc dla algorytmu kwantowego wystarczy jednokrotne wywołanie całego układu obliczeń.

Dla algorytmu potrzebna będzie dodatkowa bramka F. Dla n=2 działa ona na bity następująco:

1. dla wejścia |0⟩ ⊗ |0⟩ ⊗ |0⟩, na wyjściu pojawia się |00⟩ ⊗ |f_i(0,0)⟩
2. dla wejścia |0⟩ ⊗ |1⟩ ⊗ |0⟩, na wyjściu pojawia się |01⟩ ⊗ |f_i(0,1)⟩
3. dla wejścia |1⟩ ⊗ |0⟩ ⊗ |0⟩, na wyjściu pojawia się |10⟩ ⊗ |f_i(1,0)⟩
4. dla wejścia |1⟩ ⊗ |1⟩ ⊗ |0⟩ (gdzie x₁=1, x₂=1, y=0), na wyjściu pojawia się |11⟩ ⊗ |f_i(1,1)⟩
5. dla wejścia |0⟩ ⊗ |0⟩ ⊗ |1⟩, na wyjściu pojawia się |00⟩ ⊗ |f_i(0,0)⟩⊕1⟩
6. dla wejścia |0⟩ ⊗ |1⟩ ⊗ |1⟩, na wyjściu pojawia się |01⟩ ⊗ |f_i(0,1)⟩⊕1⟩
7. dla wejścia |1⟩ ⊗ |0⟩ ⊗ |1⟩, na wyjściu pojawia się |10⟩ ⊗ |f_i(1,0)⟩⊕1⟩
8. dla wejścia |1⟩ ⊗ |1⟩ ⊗ |1⟩, na wyjściu pojawia się |11⟩ ⊗ |f_i(1,1)⟩⊕1⟩

Znak ⊕ jest znakiem xor. Bramka jest odwracalna, gdyż np. ∣00⟩ ⊗ ∣f_i(0,0)⟩ daje ∣000> przy f_i(0,0)=0, a ∣00⟩ ⊗ ∣f_i(0,0)⊕1⟩ daje ∣001>.Z tego powodu bramka jest też kwantową bramką logiczną. Jeśli więc użyjemy bramki dwukrotnie, to druga bramka odwróci nam wartości na wartości początkowe.

Układ obliczeń

Cały układ obliczeń wygląda następująco:

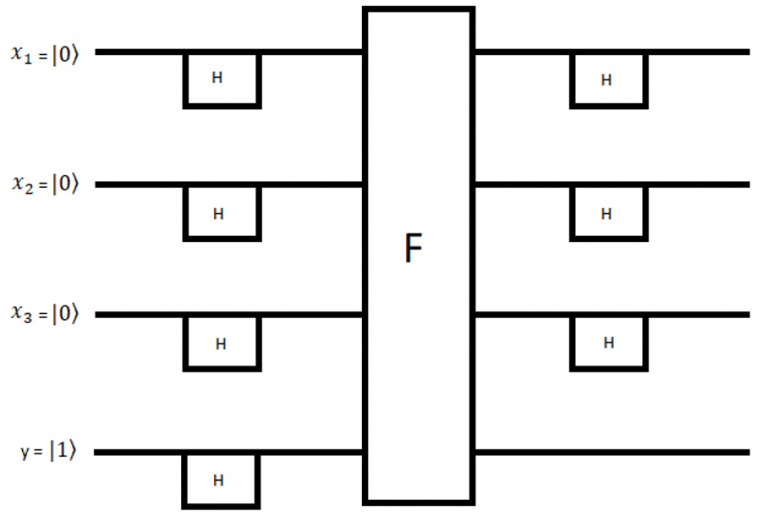
Prostokąty z literą H oznaczają bramkę Hadamarda. Prostokąt z literą F oznacza bramkę opisaną powyżej. Kubity x_i mają wartość początkową ∣0⟩. Kubit y ma wartość ∣1⟩.

Przed pierwszym przejściem przez bramkę Hadamarda układ 3 bitów x_i ma wartość ∣000⟩ Po przejściu przez pierwszą bramkę Hadamarda układ ma wartość:

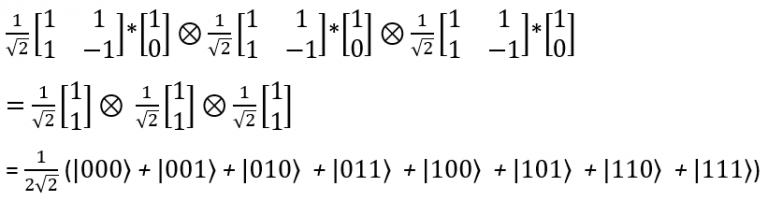
Przy kubicie y stan kubitów wygląda następująco:

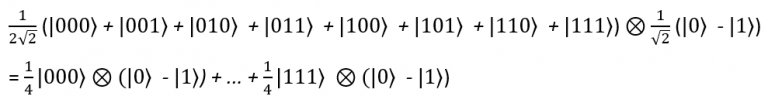
Teraz kubity przechodzą przez bramkę F, co daje:

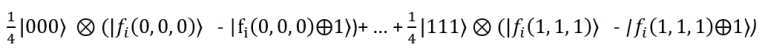
Wartość:

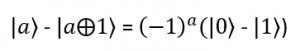
gdyż a wynosi 0 lub 1.

Można więc zapisać:

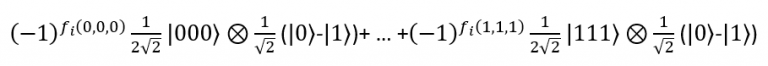
Stan kubitów dolnych to:

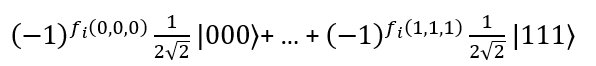
Ten stan jest superpozycją wszystkich możliwych stanów.

Teraz każdy kubit przechodzi przez kolejną bramkę Hadamarda:

Mnożąc górny wiersz przez kolumnę, otrzymamy prawdopodobieństwo stanu ∣000⟩)

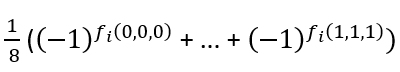
Teraz wiadomo, że:

• jeśli funkcja jest stała i przyjmuje wartość 0, to prawdopodobieństwo |000⟩ wynosi 1,
• jeśli funkcja jest stała i przyjmuje wartość 1, to prawdopodobieństwo |000⟩ wynosi -1,
• jeśli funkcja jest zbalansowana, to prawdopodobieństwo |000⟩ wynosi 0.

Teraz czas na dokonanie pomiaru kubitów x_i. Można otrzymać następujące stany:

|000>, |001>, …, |111>.

Jeśli funkcja jest stała, to prawdopodobieństwo otrzymania |000⟩ wynosi 1. W przeciwnym przypadku wynosi 0. Jeśli więc otrzymana wartość będzie wynosiła |000⟩, wtedy wiadomo, że funkcja jest stała. W tym algorytmie obliczenia wystarczyło wykonać jeden raz. W przypadku algorytmu klasycznego trzeba by użyć funkcji F nawet 5 razy.

Podsumowanie

Pisząc ten artykuł, chciałem pokazać, że informatyka kwantowa nie jest jakimś trudno dostępnym obszarem nauki. Algorytmy kwantowe różnią się od algorytmów przeznaczonych dla klasycznych komputerów, ale wynika to z innych właściwości pojedynczego nośnika informacji jakim jest kubit w porównaniu z klasycznym bitem informacji.

Myślę, że aby nabyć biegłości w używaniu i konstruowaniu programów dla komputerów kwantowych, należałoby, podobnie jak w przypadku klasycznej informatyki, odbyć studia na uczelni wyższej z tej dziedziny. Jeśli ktoś chciałby zgłębić temat, to zachęcam do przeczytania książki opisanej poniżej.

Literatura

Treść tego artykułu bazuje na informacjach zawartych w książce Chrisa Bernhadta „Obliczenia kwantowe dla każdego”. W celu ułatwienia modelu matematycznego dla obliczeń kwantowych autor nie stosuje w swojej książce liczb zespolonych, na których opierają się takie modele. Przykład algorytmu zawarty w artykule zawiera większe ilości zmiennych niż we wspomnianej literaturze przedmiotu.