Postanowiłem podzielić się moim doświadczeniem po zakończeniu projektu w obszarze bankowości (ryzyko rynkowe), gdzie używaliśmy SQL Server 2012 EE jako głównego silnika do wyliczania dwóch metryk:
- NPV (Net Present Value) – wycena produktów bankowych na wybrany moment w czasie
- EaR (Earnings at Risk) – symulacja wyceny produktów bankowych dla różnych scenariuszy zmian stóp procentowych (KNF)
Obie metryki wyliczane są na podstawie wolumenów bankowych dla różnych produktów (hipoteki, pożyczki, karty kredytowe,..), symulacji stóp procentowych oraz specyficznego czynnika dyskontującego dobranego do charakterystyki produktu. Wszystkie obliczenia wykonywane były na podstawie wzorów finansowych dostarczonych prze klienta i wymagały dużej dokładności wyników (do 13 miejsc po prawej stronie separatora dziesiętnego). W bazie przechowywaliśmy bardzo duże liczby oraz bardzo małe z dużą precyzją (skalą), więc musieliśmy określić spójny typ danych dla wszystkich wartości. Niestety nie wiedzieliśmy jakich wartości możemy się dokładnie spodziewać dla wybranych kolumn, więc musieliśmy wybrać uniwersalny typ numeryczny, który pozwoli przechowywać w tej samej kolumnie bardzo małą i dużą liczbę (0.6738230988 lub 238947783.21). Padło na typ decimal(25,13) dla procesu NPV i decimal(38,10) dla procesu EaR, żeby pokryć wszystkie przypadki i być spójnym z centralną DWH klient zarządzaną na Oracle.
I tutaj zaczynają się problemy, ponieważ SQL Server (w tym przypadku wersja 2012) nie jest dobry w obliczeniach i trzeba być bardzo świadomym, jak operacje mnożenia / dzielenia wykonywane są przez silnik bazodanowy, żeby uchronić się przed utratą precyzji danych (skali), co w konsekwencji doprowadza do dużych przekłamań w finalnych wynikach.
Całą logikę można znaleźć na stronie Microsoft i radzę każdemu dobrze się zapoznać z tym artykułem, jeżeli w Waszym projekcie dokładność obliczeń jest kluczowa!
https://docs.microsoft.com/en-us/sql/t-sql/data-types/precision-scale-and-length-transact-sql
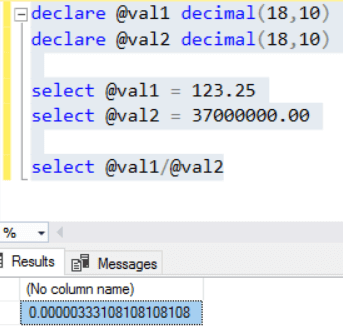
Zacznijmy od prostego przykładu.
Dostajemy wynik 0.000003 zamiast wartości jak w poniższym przykładzie Excel.
Dlaczego SQL Server nie ułatwia nam zadania i nie zadba o prawidłową precyzję, skalę wyników dla typu decimal? Niestety jeżeli dodajesz, odejmujesz, a w szczególności mnożysz i dzielisz liczby decimal, musisz liczyć się z tym, że SQL Server zwróci zaokrąglony wynik lub wynik z inna precyzją (p) i skalą (s) niż mogłoby to wynikać z danych wejściowych.
W powyższym przypadku SQL Server wykonuje następujące operacje, żeby wykonać proste dzielenie dwóch liczb decimal(p,s):
1. Wyznacza liczbę cyfr dla precyzji według wzoru: p1-s1+s2+max(6,s1+p2+1).
W naszym przypadku p=87
2. Wyznacza liczbę cyfr dla skali według wzoru: max(6,s1+p2+1).
W naszym przypadku s = 47
3. Następnie wyznacza część całkowitą według wzoru: p-s
W naszym przypadku jest to 40
4. Następnie sprawdzane są następujące warunki w celu finalnego wyznaczenia precyzji i skali (jak mocno SQL Server musi uciąć dokładność wyników po separatorze dziesiętnym):
a. Jeżeli część całkowita jest < 32 to s=min(s,38–(p-s)). Wynik może zostać zaokrąglony.
b. Jeżeli s <= 6 i p > 32 nic nie robimy ze skalą. Możemy dostać błąd „Arithmetic overflow error converting numeric to data type numeric” jeżeli wynik działania nie pasuje do decimal(38,s)
c. Jeżeli s > 6 i p > 32 to skala jest redukowana do 6 (zaokrąglona do 6 miejsc po separatorze dziesiętnym). Możemy dostać błąd „Arithmetic overflow error converting numeric to data type numeric” jeżeli część całkowita jest większa od 32 znaków.
W naszym przypadku mamy punkt (c), czyli dostajemy wynik decimal(38,6), czyli 0.000003
Żeby to naprawić musimy zmienić typ danych decimal na bardziej dokładny dla tych dwóch wartości.
Dobieranie prawidłowej precyzji, skali dla decimal może być kluczowe dla poprawności wykonywanych obliczeń i dokładności wyników. Co jeżeli nie wiemy jakich wartości możemy się spodziewać w kolumnach? Używanie typów przybliżonych w SQL Server jak float może dawać bardzo nieprecyzyjne wyniki i jest odradzane w aplikacjach finansowych (szczególnie, że wartość 0 może być przybliżone bardzo małą wartością ). Inna opcja to napisać własny CLR do wykonywania precyzyjnych obliczeń.
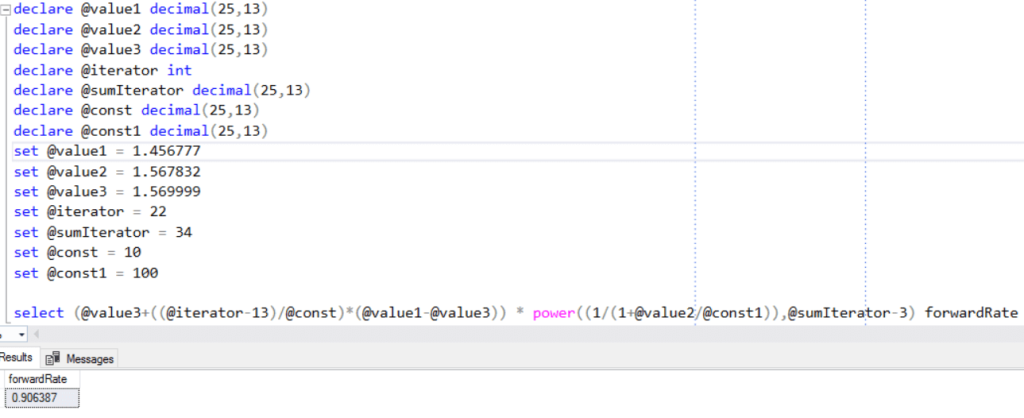
Drugi przykład demonstruje krok pośredni liczenia „forward rate” w logice symulacji stóp procentowych. Wynik powinien być bardzo dokładny i spodziewamy się 13 miejsc po separatorze dziesiętnym po wykonaniu obliczeń:
Niestety wynik znowu został zaokrąglony do 6 miejsc po separatorze dziesiętnym i trudno powiedzieć jak zmodyfikować działanie, żeby otrzymać lepszą dokładność wyniku bez zmiany typu danych dla parametrów wejściowych.
Działanie składa się z dwóch kalkulacji:
(@value3+((@iterator-13)/@const)*(@value1-@value3)) – zwracany typ decimal(38,6)
power((1/(1+@value2/@const1)),@sumIterator-3) – zwracany typ decimal(38,24)
Jeżeli teraz pomnożymy decimal(38,6) *decimal(38,24) to faktycznie dostaniemy typu decimal(38,6) jako wynik tego działania zgodnie z logiką opisaną przez Microsoft. Zakładamy, że dokładność dwóch wyników pośrednich jest zadowalająca i chcemy finalny wynik mnożenia dostać jako decimal(25,13). Co robimy? Ano kombinujemy.
Rzucamy pierwszą operację na typ decimal(25,13), żeby zredukować typ decimal(38,6)
Wynik wygląda lepiej, ale to jeszcze nie jest dokładność wyniku, o jaką nam chodzi.
Rzucamy drugą operację na typ decimal(25,13), żeby zredukować typ decimal(38,24)
Finalnie wynik wygląda poprawnie i jest to dokładność, jaką możemy dostać w Excel wykonując podobną operację (finanse zawsze porównują się do wyników z Excel).
Czyli wygląda, że w tym wypadku decimal(25,13)*decimal(25,13) daje nam decimal(25,13) ponieważ:
P=51, S=26, P-S=25, P-S<32 więc S=min(26, 38 – (51-26)) = 13
Na koniec zagadka do rozwiązania.
Dlaczego result1 != result2 mimo, że jedyna różnica w dwóch działaniach to kolejność wykonywania mnożenia, które teoretycznie nie powinno zmienić wyniku.
Który wynik jest prawidłowy? Jak wykrywać takie błędy w kodzie, jeżeli kolumny mają ten sam typ i nie bardzo wiemy, jakich wartości możemy się spodziewać w kolumnach? Dlaczego Excel daje prawidłowy wynik niezależnie od kolejności wykonywania mnożenia?
Poniżej kod, który pomoże przygotować dane.
if object_id(’tempdb..#test’) is not null
drop table #test
select * into #test
from
(
select cast(1.8100000000000 as decimal(25,13)) forwardRateForInterest,
cast(0.0000000000000 as decimal(25,13)) Additiv_Mrgn_Pnt,
cast(100.0000000000000 as decimal(25,13)) cnt1,
cast(100.0000000000000 as decimal(25,13)) cnt2,
cast(0.5013698630137 as decimal(25,13)) YF_I,
cast(17300000.0000000000000 as decimal(25,13)) Nom_PLN)a
–select name, type_name(system_type_id) type, precision, scale
–from tempdb.sys.columns where [object_id] = object_id(N’tempdb..#test’);
select
((forwardRateForInterest + Additiv_Mrgn_Pnt/cnt1)/cnt2) * Nom_PLN*YF_I result1,
((forwardRateForInterest + Additiv_Mrgn_Pnt/cnt1)/cnt2) * YF_I*Nom_PLN result2
from #test
Podsumowując:
- Zapoznaj się z artykułem https://docs.microsoft.com/en-us/sql/t-sql/data-types/precision-scale-and-length-transact-sql żeby być świadomym jak SQL Server ustala typ danych dla wyników działań arytmetycznych.
- Jeżeli jest to możliwe, używaj bardzo precyzyjnych typów danych. Precyzja i skala typu decimal powinna być dobrana pod rzeczywiste dane.
- Uważaj na typ float, który przechowuje przybliżone wartości liczb (0 może nie być zerem).
- Jeżeli jest to możliwe, bardzo skomplikowane obliczenia wykonuj w CLR.
- Złośliwi koledzy z pokoju radzą zacząć używać Oracle, który lepiej radzi sobie z liczbami i operacjami arytmetycznymi.



















Zostaw komentarz