W trakcie rozwoju oprogramowania niejednokrotnie zachodzi potrzeba wdrożenia projektu mimo istniejących, nierozwiązanych błędów.
Zwykle dzieje się to w wyniku presji czasu. Wraz z rozwojem elektroniki można spodziewać się, że sytuacja powyższa może dotknąć również procesorów. W architekturze x86 na przestrzeni kilkudziesięciu lat wykryto pewną liczbę błędów, od bardzo poważnych luk bezpieczeństwa (jak Spectre i Meltdown), po takie, których przeciętny użytkownik może nigdy nie zauważyć (jak FDIV – niedokładność przy dzieleniu liczb zmiennoprzecinkowych). W tym artykule przybliżone będzie inne, mniej znane zachowanie FPU mające wpływ na dokładność operacji sinus oraz cosinus. Choć zalicza się do tych na ogół o mniejszym wpływie, może jednak przyprawić programistę o ból głowy, szczególnie jeśli zależy mu na dużej dokładności obliczeń. Na ten błąd autor natknął się podczas testowania sterownika PLC i było zaskakujące jak duża może być skala błędu.
Liczby stało- a zmiennoprzecinkowe
Na komputerach, które wszyscy znamy, tj. operujących w systemie binarnym można wykonywać działania na liczbach całkowitych, stało- lub zmiennoprzecinkowych. Pierwszych z nich na łamach tego bloga nie trzeba szczególnie wyjaśniać. Stałoprzecinkowe, podobnie jak całkowite, na kolejnych bitach przechowują kolejne potęgi dwójki, np. 110101,11b = 25+24+22+20+2-1+2-2 = 53,75. Takie typy można spotkać np. w bibliotece CMSIS DSP, gdzie zdefiniowane są: Q7, Q15 oraz Q31. Jeden bit przechowuje w nich znak, a pozostałe stanowią część ułamkową. W przypadku wartości ujemnych obowiązuje w nich uzupełnienie do dwóch, zatem 11111111b w typie Q7 odpowiada liczbie -1/128.
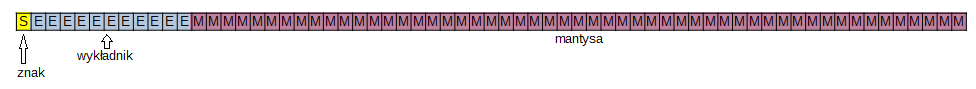
Liczby zmiennoprzecinkowe to osobna koncepcja zdefiniowana w normie IEEE-754. Koduje się je przy pomocy trzech pól bitowych: znaku, wykładnika i mantysy, stosując do nich specjalne reguły. Mianowicie, wykładnik dla typu double składa się z jedenastu bitów. Najmniejszy możliwy wykładnik, (tj, -1022) jest kodowany w postaci: 00000000001b, natomiast najwyższy możliwy, jako: 11111111110b. Mantysa przechowuje liczbę podobnie jak liczby stałoprzecinkowe, jednak z pominięciem jedynki na najstarszym bicie. Przyjmuje się, że liczba różna od zera zawsze tę jedynkę musi mieć, stąd dobiera się wykładnik tak, aby jedynkę wysunąć na bit o jeden wyższy niż liczba bitów mantysy. Proces ten nazywa się normalizacją, a wspomniany bit musi być uwzględniony przy wszystkich działaniach. Gdy wynik jest zbyt mały, aby dało się spełnić ten warunek w wykładniku pojawiają się same zera a liczby z tego nazywa się nieznormalizowanymi. Mantysa reprezentuje wtedy liczbę postaci 0,xxx…xxx, zamiast 1,xxx…xxx.
Liczba zmiennoprzecinkowa może przechowywać liczby od niewielkich ułamków po bardzo duże wartości: 3.4E+38 dla liczb pojedynczej precyzji i +1.7E+308 dla podwójnej precyzji. Aby uzmysłowić sobie jak duże to liczby, warto posłużyć się przykładem: szacuje się, że we wszechświecie znajduje się między 1078 a 1082 atomów. Z drugiej strony obydwa te typy zajmują odpowiednio 32 i 64 bity. Wynikają z tego dwa fakty:
- Liczba zmiennoprzecinkowa może przechować tylko tyle różnych wartości ile odpowiadające im uint32_t i uint64_t. Ponieważ 232 < 3.4E+38 oraz 264 < +1.7E+308, wiele pośrednich wartości nie może być zapisanych przy pomocy tego typu.
- Używając unii języka C możemy mieć dostęp do reprezentacji bitowej liczby zmiennoprzecinkowej. Istotnie, sąsiadujące ze sobą wartości float czy double w reprezentacji bitowej uintNN_t będą też kolejnymi, sąsiadującymi ze sobą liczbami całkowitymi.
Tę drugą właściwość wygodnie jest użyć do porównywania. Np. znając dokładny, spodziewany wynik, aby sprawdzić dokładność danej operacji wystarczy odjąć reprezentacje bitowe obu liczb. Jednostkę otrzymanego wyniku określa się angielskim skrótowcem ULP (units in the last place). Przez wiele lat dokładność instrukcji FSIN w podręczniku dla architektury Intela była określona jako nie większa niż 2 ULP. Czy tak jest w istocie?
Operacja FSIN
Funkcje trygonometryczne można obliczyć w sposób analityczny dzięki aproksymacji. Obliczenie odbywa się zwykle w dwóch etapach:
- argument, jeśli wykracza poza podstawowy okres, dla którego dokonano aproksymacji, jest redukowany do tego podstawowego zakresu. Realizuje się tę redukcję poprzez odjęcie wielokrotności liczby π od argumentu, np. 3/2 π będzie zredukowane do ½ π
- tak zredukowany argument jest podawany na wejście funkcji aproksymującej sinus przy pomocy np. wielomianu (inna technika, często implementowana w sprzęcie to CORDIC)
Przy wystarczająco dokładnej aproksymacji i niewielkim argumencie dokładność może być taka jak to było zapowiedziane. Źródłem niedokładności jest wspomniana wyżej redukcja argumentu. Przy tej redukcji wykorzystywana jest stała π, zapisana w strukturze koprocesora arytmetycznego w postaci 66-bitowej stałej. To za mało aby uzyskać dokładny wynik. Zobaczmy to na przykładzie liczby podwójnej precyzji bliskiej π (typu double – rozmiar mantysy wynosi wtedy 53 bity).

Różnica między argumentem z 53 bitami mantysy a wyżej wspomnianą aproksymacją da jedynie 13 bitów dokładnego wyniku. Dodatkowo, im większy argument tym błąd będzie się kumulował.
Podsumowanie
W przypadku tej nieprawidłowości zdecydowano na dodanie dokładniejszego wyjaśnienia nt. precyzji w dokumentacji zamiast poprawki w sprzęcie, najprawdopodobniej z powodu kompatybilności. W ten sposób uniknięto sytuacji, w której procesory z tej samej rodziny generują różne wyniki. Błędy, o których mowa, mają duże wartości względne, ale w liczbach bezwzględnych są to niewielkie liczby, bliskie zeru. Przypuszczam, że taki jest powód, dla którego nie dostrzeżono tego błędu w czasie produkcji i to za tym stała taka, a nie inna decyzja producenta w sprawie odpowiedzi na zgłoszenie błędu. Należy zatem pomyśleć o tym, aby ograniczyć argument wejściowy, w celu ograniczenia błędów numerycznych, które wnoszą funkcje trygonometryczne.
Warto wspomnieć, że systemy uniksowe nie wywołują na ogół instrukcji FSIN, ponieważ w bibliotece GLIBC znajduje się implementacja omijająca FPU. Jak podaje Jason Orendorff na Stack Overflow, jest ona szybsza niż obliczenie z wykorzystaniem koprocesora (za to błędy ULP porównywalne).
Bibliografia
- Lista błędów procesorów x86: https://wiki.osdev.org/CPU_Bugs
- Szczegółowy artykuł Bruce’a Dawsona na ten sam temat: https://randomascii.wordpress.com/2014/10/09/intel-underestimates-error-bounds-by-1-3-quintillion/
- Odpowiedź Intela na zgłoszone nieprawidłowości: https://software.intel.com/blogs/2014/10/09/fsin-documentation-improvements-in-the-intel-64-and-ia-32-architectures-software
- Dokumentacja procesorów Intel (Software Developer’s Manual): https://software.intel.com/content/dam/develop/public/us/en/documents/325462-sdm-vol-1-2abcd-3abcd.pdf
- Wizualne przedstawienie precyzji funkcji trygonometrycznych dla architektur x86: http://notabs.org/fpuaccuracy/index.htm
- Pytanie ze Stack Overflow nt. Implementacji funkcji trygonometrycznych: https://stackoverflow.com/questions/2284860/how-does-c-compute-sin-and-other-math-functions
Przykładowy kod umożliwiający samodzielne sprawdzenie prezentowanych tutaj rewelacji: https://gitlab.com/skocjan/sin_fpu.git
















Zostaw komentarz